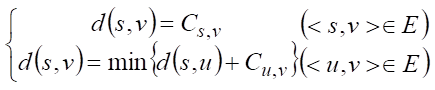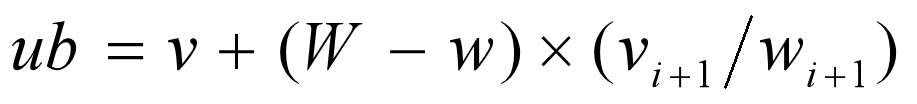引言

快要期末考试啦，对算法做一个总结，以备自己后续的学习。

看之前可以先重点看看目录，这样可以明确这篇文章的结构，并且迅速找到需要的知识

算法基础知识

算法的五个特性：（必考）

  1. 输入
  2. 输出
  3. 有穷
  4. 可行
  5. 确定

常用的描述算法的方法：

  • 自然语言
  • 流程图
  • 伪代码
  • 程序设计语言

时间复杂度：

​ 概念：

  • O(n):用来描述增长率的上限
  • Ω(n):用来描述增长率的下限

最优算法：大Ω符号常常与大O符号配合以证明某问题的一个特定算法是该问题的最优算法，或是该问题中的某算法类中的最优算法。一般情况下，如果能够证明某问题的时间下界是Ω(g(n))来求解该问题的任何算法，都认为是求解该问题的最优算法

主定理：

在这里插入图片描述

习题：

基本的算法设计技术

分治法与减治法

基本思路：

​ 分治法：将一个难以直接解决的大问题划分成一些规模较小的子问题，分别求解各个子问题，然后将各个子问题的解合并。分为三步：划分、求解子问题、合并。

​ 减治法：将一个难以直接解决的大问题划分为若干子问题，但是这些子问题不需要分别求解，只需求解其中的一个子问题，因而也就无需对子问题的解进行合并。

同与异：

同：都需要划分子问题，都需要求解子问题;它俩的编程思想都是递归

异：减治法无须合并子问题，只需要找出子问题的解与原问题解之间的对应关系，或直接求解子问题便得原问题的解。

适用范围：

分治法：最好使子问题的规模大致相同（子问题平衡）

应用：

​ 分治法：

  1. 归并排序
  2. 快速排序

​ 减治法：

  1. 折半查找
  2. 二叉查找树
  3. 堆排序

对于排序与查找算法没有最好的，只有最合适的。

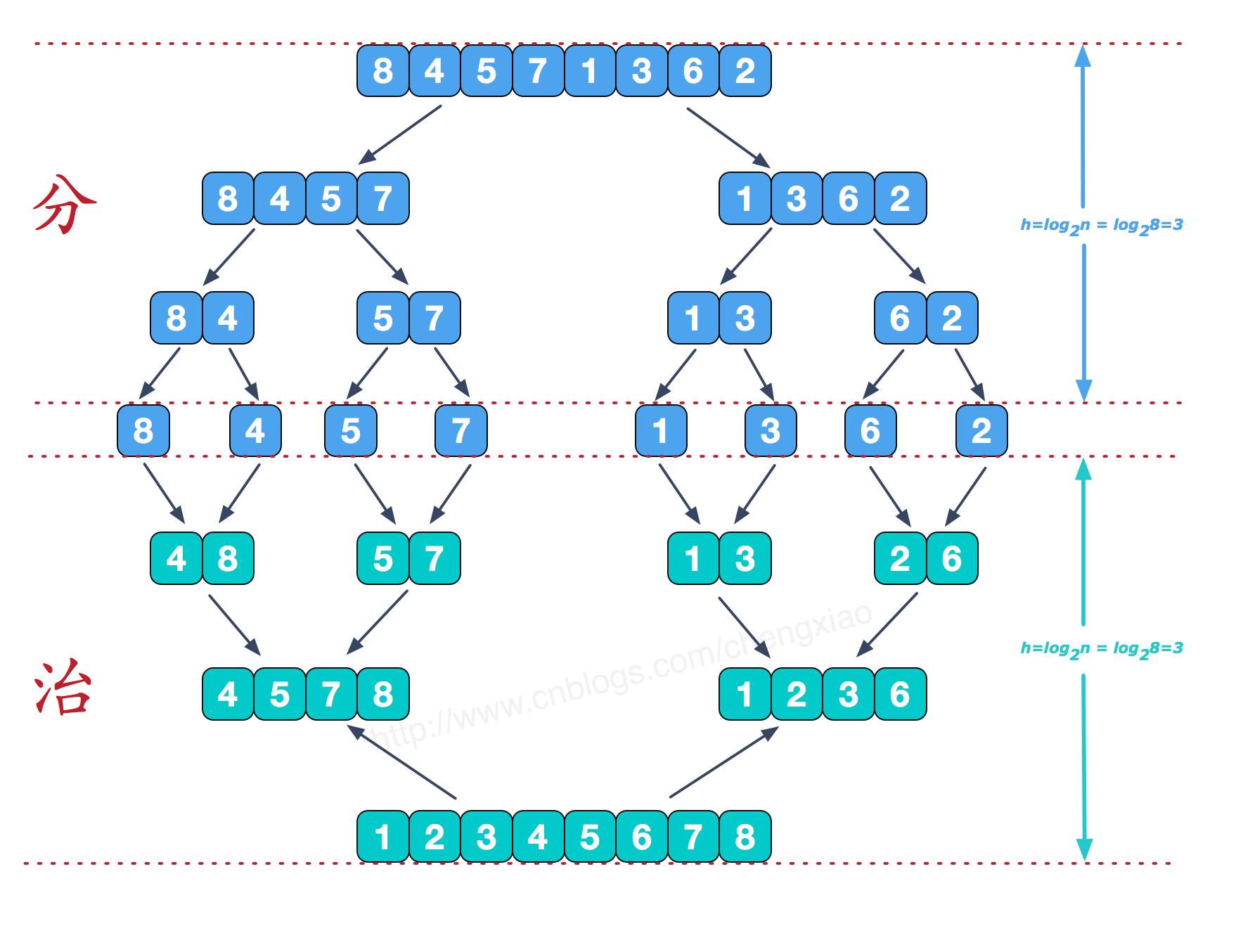
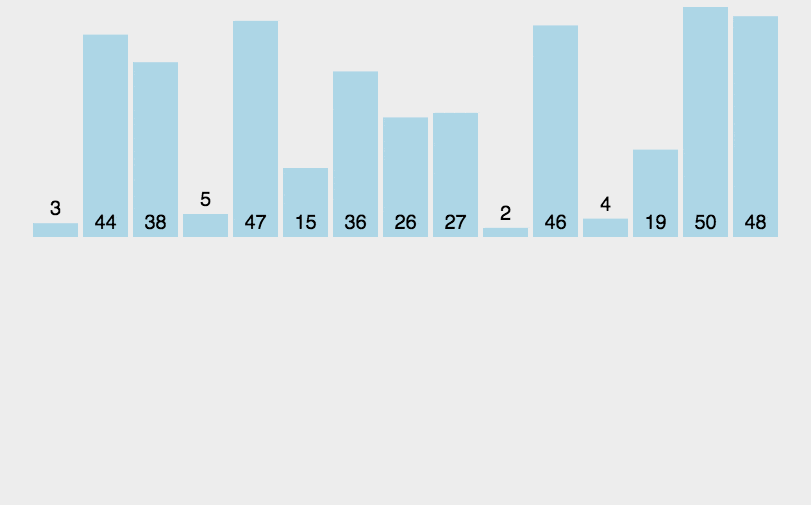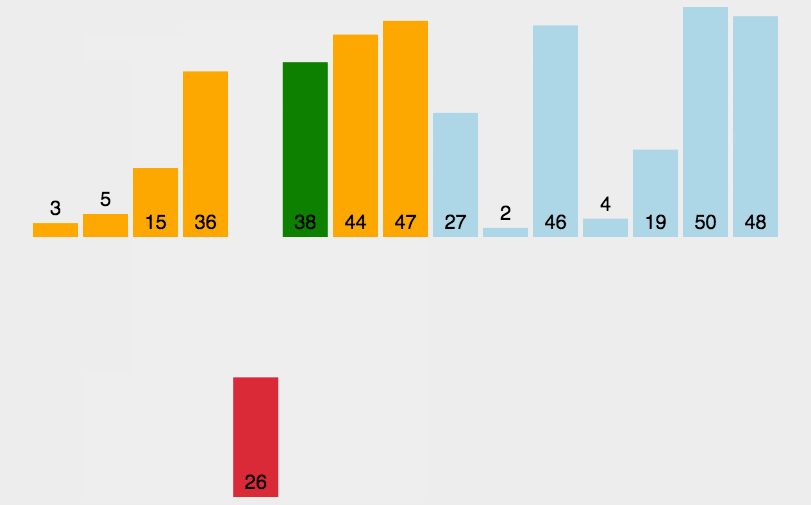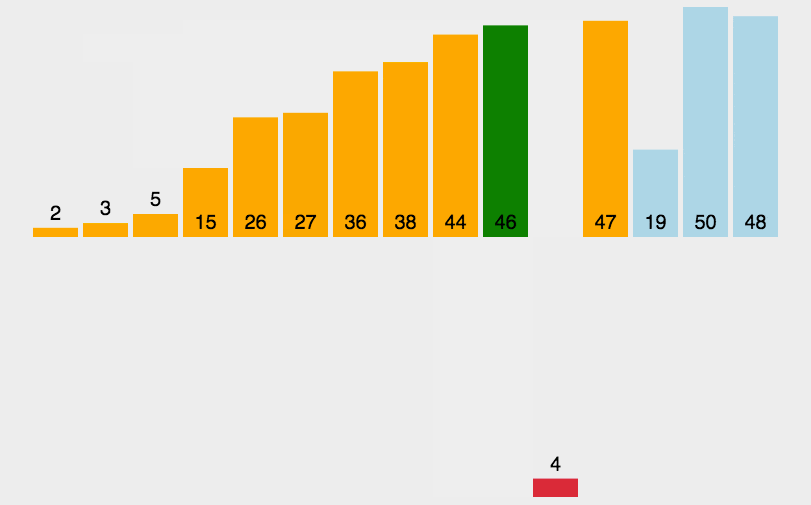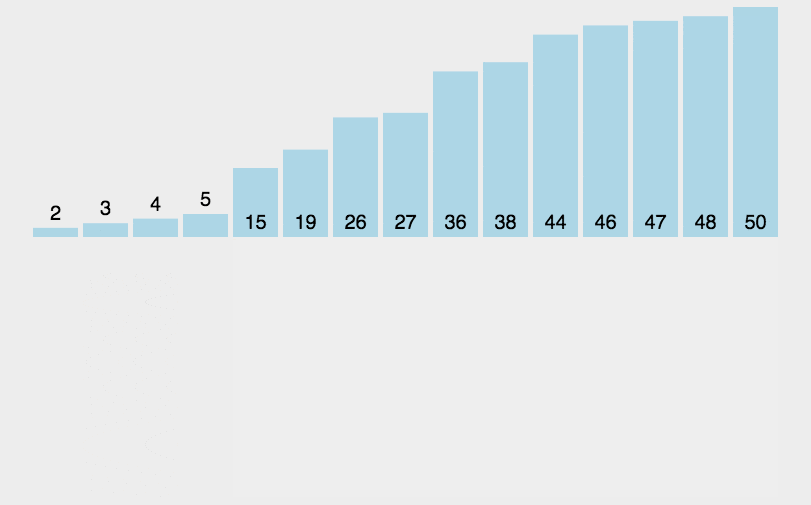
归并排序

核心思想：

不断地将序列一分为二（若是奇数个数则向上取整，例如7/2=3.5向上取整则为4，因此左边四个数，右边三个数）直至分到只有一个数为止，然后开始合并并排序 。

详细解读：1557906108-5066-20161218163120151-452283750

首先是分然后是治，先不断地一分为二，然后不断地合二为一。

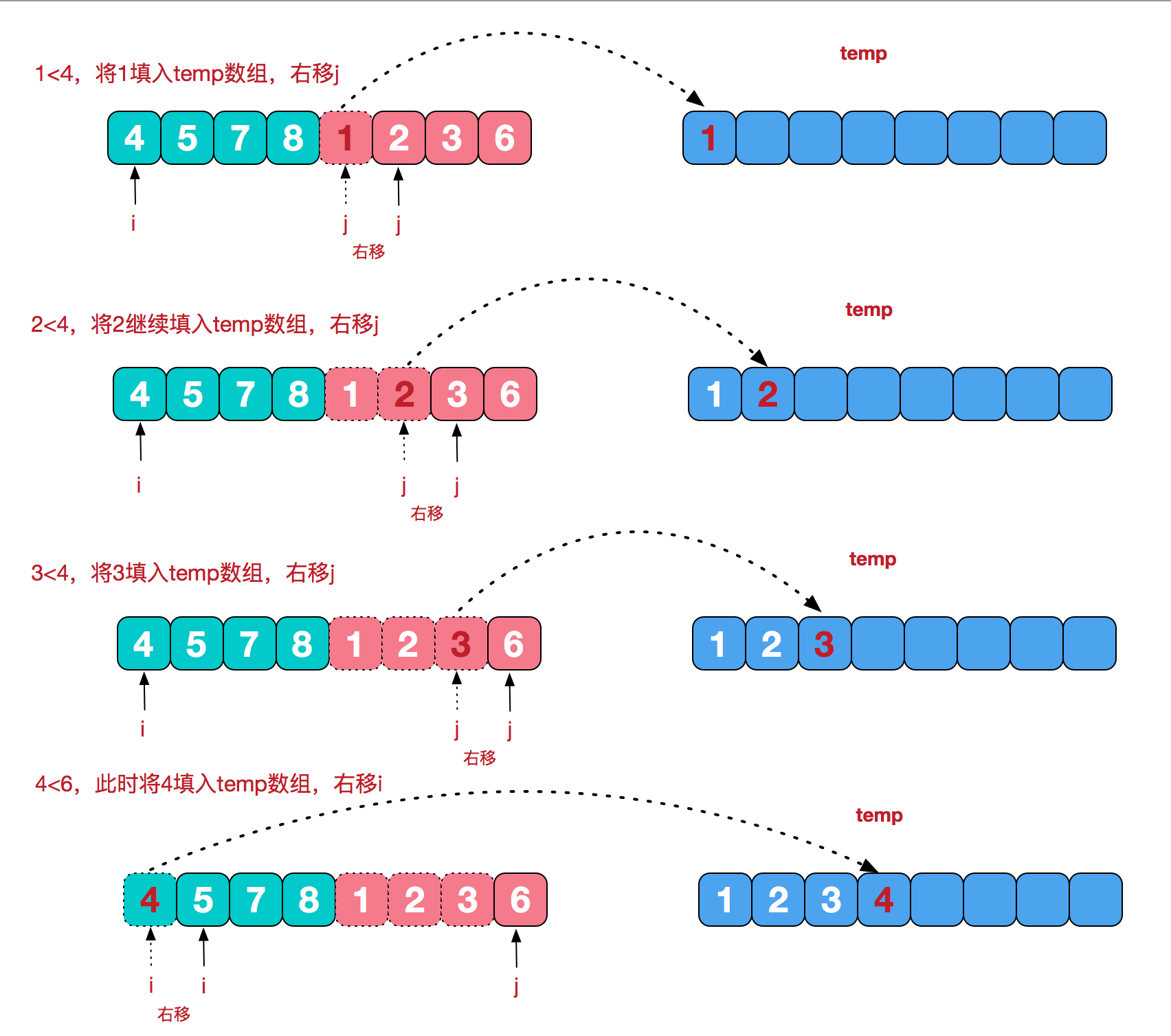
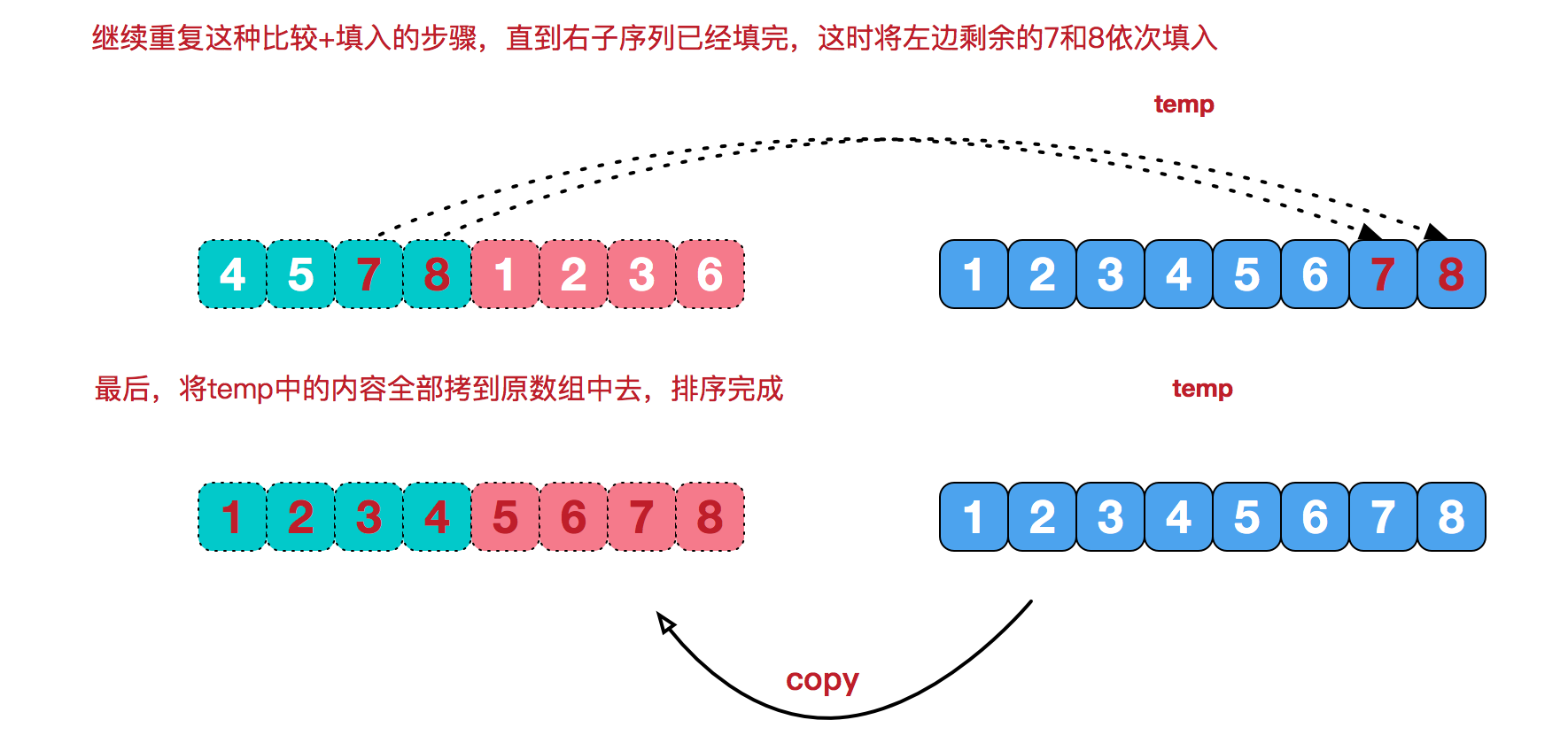
我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现合并的步骤。

1557906108-2034-20161218194508761-4681695401557906108-7614-20161218194621308-588010220

下面是两个应用，一个为偶序列，一个为奇序列

请添加图片描述

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void merge_sort(int *data, int start, int end, int *result)
{
    if(1 == end - start)//如果区间中只有两个元素，则对这两个元素进行排序
    {
        if(data[start] > data[end])
        {
            int temp  = data[start];
            data[start] = data[end];
            data[end] = temp;
        }
        return;
    }
    else if(0 == end - start)//如果只有一个元素，则不用排序
        return;
    else
    {
        //继续划分子区间，分别对左右子区间进行排序
        merge_sort(data,start,(end-start+1)/2+start,result);
        merge_sort(data,(end-start+1)/2+start+1,end,result);
        //开始归并已经排好序的start到end之间的数据
        merge(data,start,end,result);
        //把排序后的区间数据复制到原始数据中去
        for(int i = start;i <= end;++i)
            data[i] = result[i];
    }
}

merge的过程为： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void merge(int *data,int start,int end,int *result)
{
    int left_length = (end - start + 1) / 2 + 1;//左部分区间的数据元素的个数
    int left_index = start;
    int right_index = start + left_length;
    int result_index = start;
    while(left_index < start + left_length && right_index < end+1)
    {
        //对分别已经排好序的左区间和右区间进行合并
        if(data[left_index] <= data[right_index])
            result[result_index++] = data[left_index++];
        else
            result[result_index++] = data[right_index++];
    }
    while(left_index < start + left_length)
        result[result_index++] = data[left_index++];
    while(right_index < end+1)
        result[result_index++] = data[right_index++];
}

现在对程序进行测试： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int main()
{
    int data[] = {9,6,7,22,20,33,16,20};
    const int length = 8;
    int result[length];
    cout << "Before sorted:" << endl;
    for(int i = 0;i < length;++i)
        cout << data[i] << "  ";
    cout << endl;
    cout << "After sorted:" << endl;
    merge_sort(data,0,length-1,result);
    for(int i = 0;i < length;++i)
        cout << data[i] << "  ";
    cout << endl;

    return 0;
}

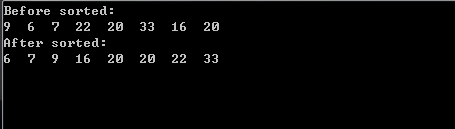
运行结果：

img

总结：

归并排序的性能不受输入数据的影响，始终都是 O(nlogn) 的时间复杂度。代价是需要额外的内存空间。

快速排序：

核心思想

快速排序算法的思想非常简单，在待排序的数列中，我们首先要找一个数字作为基准数（这只是个专用名词）。为了方便，我们一般选择第 1 个数字作为基准数（其实选择第几个并没有关系）。接下来我们需要把这个待排序的数列中小于基准数的元素移动到待排序的数列的左边，把大于基准数的元素移动到待排序的数列的右边。这时，左右两个分区的元素就相对有序了；接着把两个分区的元素分别按照上面两种方法继续对每个分区找出基准数，然后移动，直到各个分区只有一个数时为止。

因此可以总结为三点：

  • 1．先从数列中取出一个数作为基准数。
  • 2．分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。
  • 3．再对左右区间重复第二步，直到各区间只有一个数。

那么移动元素，该怎么移动呢？

快速排序的操作是这样的：首先从数列的最右边（也就是最后一个数字）开始往左边找，我们设这个下标为 j，也就是进行减减操作（j–），找到第 1 个比基准数小的值，让它与基准值交换；接着从左边开始往右边找，设这个下标为 i，然后执行加加操作（i++），找到第 1 个比基准数大的值，让它与基准值交换；然后继续寻找，直到 i 与 j 相遇时结束，最后基准值所在的位置即 k 的位置，也就是说 k 左边的值均比 k 上的值小，而 k 右边的值都比 k 上的值大。

详细解读：

请添加图片描述

代码：（Java版）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
public class QuickSort {
    private int[] array;
    public QuickSort(int[] array) {
        this.array = array;
    }
    public void sort() {
        quickSort(array, 0, array.length - 1);
    }
    public void print() {
        for (int i = 0; i < array.l	ength; i++) {
            System.out.println(array[i]);
        }
    }
   
    /**
     * 递归排序
     * @param src
     * @param begin
     * @param end
     */
    private void quickSort(int[] src, int begin, int end) {
        if (begin < end) {
            int key = src[begin];
            int i = begin;
            int j = end;
            while (i < j) {
                while (i < j && src[j] > key) {
                    j--;
                }
                if (i < j) {
                    src[i] = src[j];
                    i++;
                }
                while (i < j && src[i] < key) {
                    i++;
                }
                if (i < j) {
                    src[j] = src[i];
                    j--;
                }
            }
            src[i] = key;
            quickSort(src, begin, i - 1);
            quickSort(src, i + 1, end);
        }
    }
}

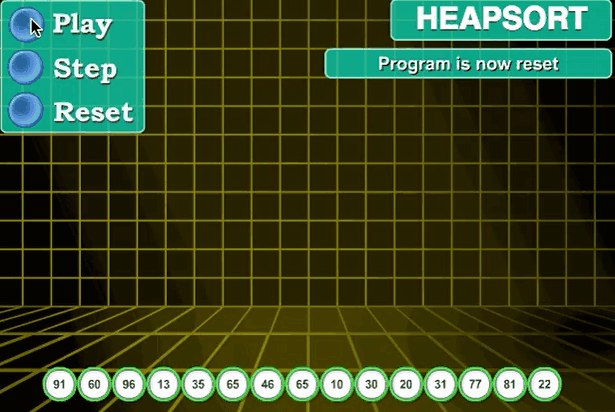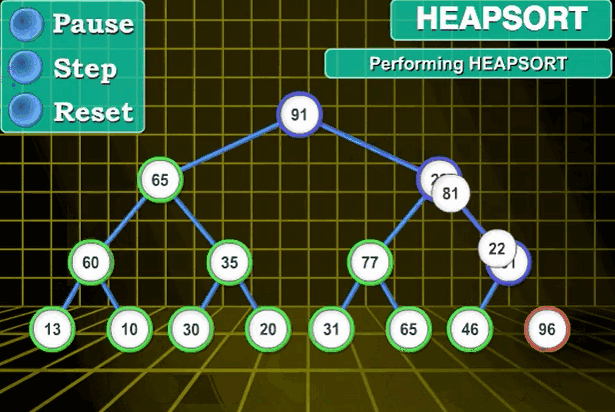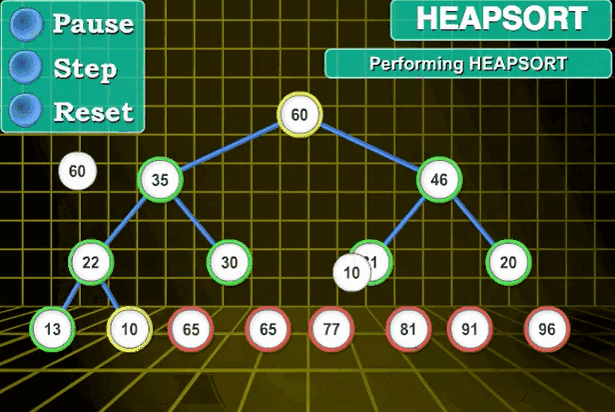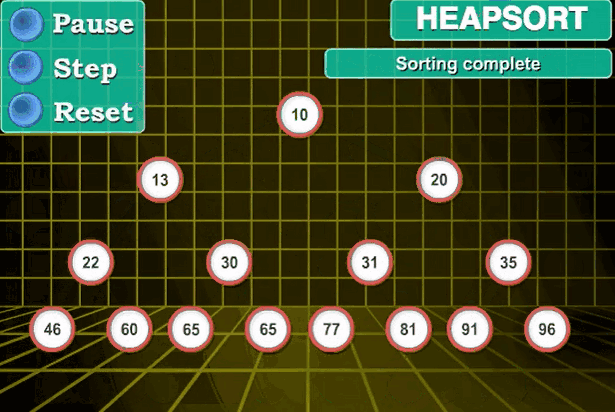
堆排序：

核心思想：

​ 堆排序中的“堆”的含义是完全二叉树。算法的具体操作步骤分为4步：

  1. 先将无序序列画成一个完全二叉树的形式
  2. 再自底向上，自右向左对完全二叉树中的元素进行比较得到大根堆或小根堆
  3. 然后将完全二叉树的根节点与堆中最右下角的元素互换，互换之后根节点脱落，从此此根节点不再参与比较，而是等待之后的根节点相继脱落一起形成有序区。
  4. 之后一种重复2,3步便可得到有序区（有序序列）。

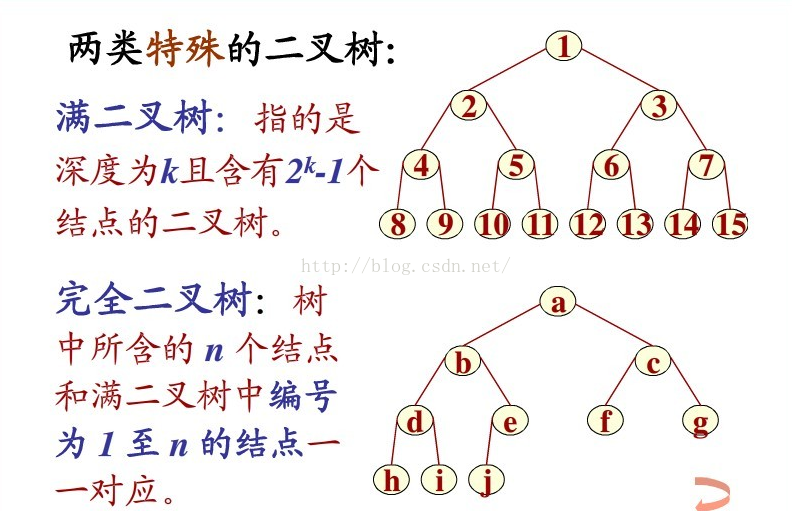
这里说一下什么是完全二叉树，同时也区分一下完全二叉树与满二叉树的区别

先看图：

img

完全二叉树：设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，
第 h 层所有的结点都连续集中在最左边（例如如果在上图的完全二叉树的g结点接一个k结点，则这个数便不再是完全二叉树）

满二叉树：深度为k且有2^k-1个结点的二叉树称为满二叉树

详细解读：

img

代码：（C++）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <iostream>
#include <algorithm>
using namespace std;
void max_heapify(int arr[], int start, int end) {
    //建立父节点指标和子节点指标
    int dad = start;
    int son = dad * 2 + 1;
    while (son <= end) { //若子节点指标在范围内才做比较
        if (son + 1 <= end && arr[son] < arr[son + 1]) //先比较两个子节点大小，选择最大的
            son++;
        if (arr[dad] > arr[son]) //如果父节点大于子节点代表调整完毕，直接跳出函数
            return;
        else { //否则交换父子内容再继续子节点和孙节点比较
            swap(arr[dad], arr[son]);
            dad = son;
            son = dad * 2 + 1;
        }
    }
}
void heap_sort(int arr[], int len) {
    //初始化，i从最后一个父节点开始调整
    for (int i = len / 2 - 1; i >= 0; i--)
        max_heapify(arr, i, len - 1);
    //先将第一个元素和已经排好的元素前一位做交换，再从新调整(刚调整的元素之前的元素)，直到排序完毕
    for (int i = len - 1; i > 0; i--) {
        swap(arr[0], arr[i]);
        max_heapify(arr, 0, i - 1);
    }
}
int main() {
    int arr[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
    int len = (int) sizeof(arr) / sizeof(*arr);
    heap_sort(arr, len);
    for (int i = 0; i < len; i++)
        cout << arr[i] << ' ';
    cout << endl;
    return 0;
}

总结：

​ 堆是一种很好做调整的结构，在算法题里面使用频度很高。常用于想知道最大值或最小值的情况，比如优先级队列，作业调度等场景。堆排序的时间性能是O(logn)

折半查找：

核心思想：

​ 在一个有序表中，每次取目标值与序列中间的值进行比较。若目标值等于值，则查找成功，返回此值的位置；若目标值大于此值，则说明目标值在该查找表的右半区，此时我们往右半区进行查找；若目标值小于此值，则说明目标值在该查找表的右左半区此时我们往左半区进行查找。如此往复，直至查找成功；若无和目标值相等的记录数，则查无此值。

详细解读：

img

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <stdio.h>
#include <stdlib.h>

//折半查找,又称为二分查找 ,条件保证要好排序的，不适合应用在频繁的插入操作，因为会打乱顺序
int Binary_Search(int *a,int n,int key)
{
    int low,high,mid;
    low = 0;    //定义最低下标为记录首位
    high = n;   //记录最高下标为记录末位

    while ( low <= high )
    {
        mid = (low + high) / 2;
        if (key < a[mid]) {
            high = mid - 1;//最高位下标调小 一位
        }
        else if(key > a[mid]){
            low = mid + 1; //最低下标调整到中位下标大一位
        } 
        else{
            return mid; //代表就是次位置
        }
    }
    return -1; //没有找到返回-1
}

void main()
{
    int a[] = {1,2,3,4,5,6,7,8,9,10};

    //需求要查找8, 如果用传统的方式 要查找8次才能得出
    int index;//下标
    index = Binary_Search(a, sizeof(a) / sizeof(int),8);

    if (index == -1)
        printf("没有找到");
    else
        printf("找到了,index为:%d",index);
}

总结：

     二分查找有个很重要的特点，就是不会查找数列的全部元素，而查找的数据量其实正好符合元素的对数，正常情况下每次查找的元素都在一半一半地减少。所以二分查找的[时间复杂度](http://data.biancheng.net/view/2.html)为 `O(log2n)` 是毫无疑问的。当然，最好的情况是只查找一次就能找到，但是在最坏和一般情况下的确要比顺序查找好了很多。

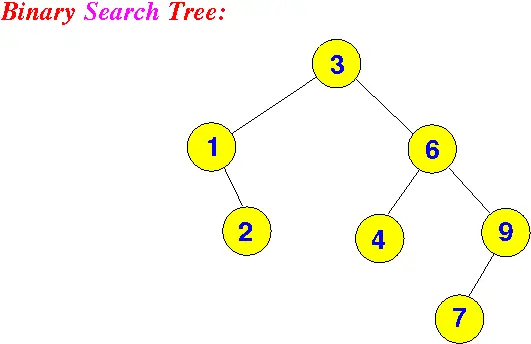
二叉查找树（二叉搜索树）：

核心思想：

​ 左右子树与根节点的关系（左子树比根节点都小，右子树比根节点都大）

详细解读：v2-a979f7099bf4d4d62ad2ab3ef8c95baa_b

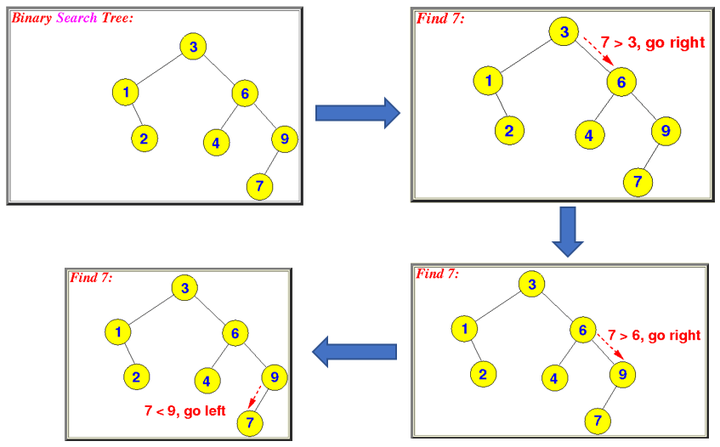
在BST中搜索一个值是非常简单和高效的。

v2-b45aa1eee3d524e00d4207f81fcadb19_720w

看上面的树，假设要搜索7这个节点。首先从Root节点出发，我们知道7大于3，所以会走到右子树6，然后因为7也大于6，所以会继续往右子树走，到了9，因为7小于9，所以会向左子树走，走到7，发现7等于7，所以找到要搜索的节点。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
// 这里先定义出节点的结构
class Node
{
    public int data;
    public Node parent;
    public Node left;
    public Node right;

    public Node(int _data)
    {
        this.data = _data;
    }
}

// 定义二叉搜索树结构
class BST
{
    private Node root;

    // 这个函数是 private 的，递归调用，插入节点
    private Node RecursionInsert(Node node, int data)
    {
        if (node == null)
        {
            return new Node(data);
        }

        if (data < node.data)
        {
            node.left = RecursionInsert(node.left, data);
            node.left.parent = node;
        }
        else if (data > node.data)
        {
            node.right = RecursionInsert(node.right, data);
            node.right.parent = node;
        }

        return node;
    }

    // 对外开放的 插入 接口
    public void Insert(int data)
    {
        if (root == null)
        {
            root = RecursionInsert(root, data);
        }
        else
        {
            RecursionInsert(root, data);
        }
    }

    // 按层序打印二叉树
    public void LevelOrderTraversal()
    {
        Queue<Node> q = new Queue<Node>();
        q.Enqueue(root);

        while (q.Count > 0)
        {
            Node currNode = q.Dequeue();

            if (currNode.left != null)
            {
                q.Enqueue(currNode.left);
            }

            if (currNode.right != null)
            {
                q.Enqueue(currNode.right);
            }
            // 括号里面是父节点的值
            string msg = string.Format("{0}({1})", currNode.data, currNode.parent != null ? currNode.parent.data.ToString() : "null");
            Debug.Log(msg);
        }
    }
}

// 创建一个二叉搜索树
class Program
{
    /* Let us create following BST
          50
       /     \
      30      70
     /  \    /  \
   20   40  60   80 */

    static void Main(string[] args)
    {
        BST bst = new BST();
        bst.Insert(50);
        bst.Insert(30);
        bst.Insert(20);
        bst.Insert(40);
        bst.Insert(70);
        bst.Insert(60);
        bst.Insert(80);

        bst.LevelOrderTraversal();
    }
}

总结

二叉查找树查找成功的平均查找长度为: ASL = [ (n+1)/n] * log2 (n+1) - 1 [公式1] 其时间复杂度是: O (log2 (n))

插入排序：

核心思想：

打扑克＋遍历，打过扑克的朋友对于理解这个排序应该是手到擒来的，我们在摸牌阶段要不断调整牌的顺序，每次摸一张牌查到原来序列当中，其操作流程就是与每一张牌比大小然后放在比它大的牌前面。

详细解读：insertionSort

代码:

1
2
3
4
5
6
7
8
9
10
11
void insertion_sort(int arr[],int len){
        for(int i=1;i<len;i++){
                int key=arr[i];
                int j=i-1;
                while((j>=0) && (key<arr[j])){
                        arr[j+1]=arr[j];
                        j--;
                }
                arr[j+1]=key;
        }
}

总结：

插入排序的时间复杂度为O(n^2)

动态规划法与贪心法

基本思路：

动态规划法：

  1. 划分子问题

    将原问题分解为若干个子问题，并且子问题之间具有重叠关系（交集）

  2. 确定动态规划函数

    根据子问题之间的重叠关系，找出满足子问题的递推关系式（即动态规划函数），此乃动态规划法之关键，找递归关系式往往需要自顶向下

  3. 填写表格

    以自底向上的方式计算各个子问题的解并填表，实现动态规划过程

贪心法：其核心便是四个字“目光短浅”，即在解决问题时，只根据当前已有的信息做出最优选择，而不管将来有什么选择，因此其算法希望通过局部最优的选择达到全局最优的选择 。

同与异：

同：要求原问题必须有最优子结构。

异：贪心法的计算方式“自顶向下”，但并不等待子问题求解完毕后再选择使用哪一 个，而是通过一种策略直接选择一个子问题去求解，没被选择的子问题直接抛 弃。这种所谓“最优选择”的正确性需要用归纳法证明。而动态规划不管是采用 自底向上还是自顶向下的计算方式，都是从边界开始向上得到目标问题的解 （即考虑所有子问题）。

贪心：壮士断腕的决策，只要选择，绝不后悔。

动态规划：要看哪个选择笑到最后，暂时领先说明不了问题。

适用范围：

动态规划：多用来解决多阶段决策最优化（最值与优化）问题。

贪心法：求解最优化问题，而且对于许多问题都能都到整体最优解，即使不能得到整体最优解，通常也是最优解的很好近似。

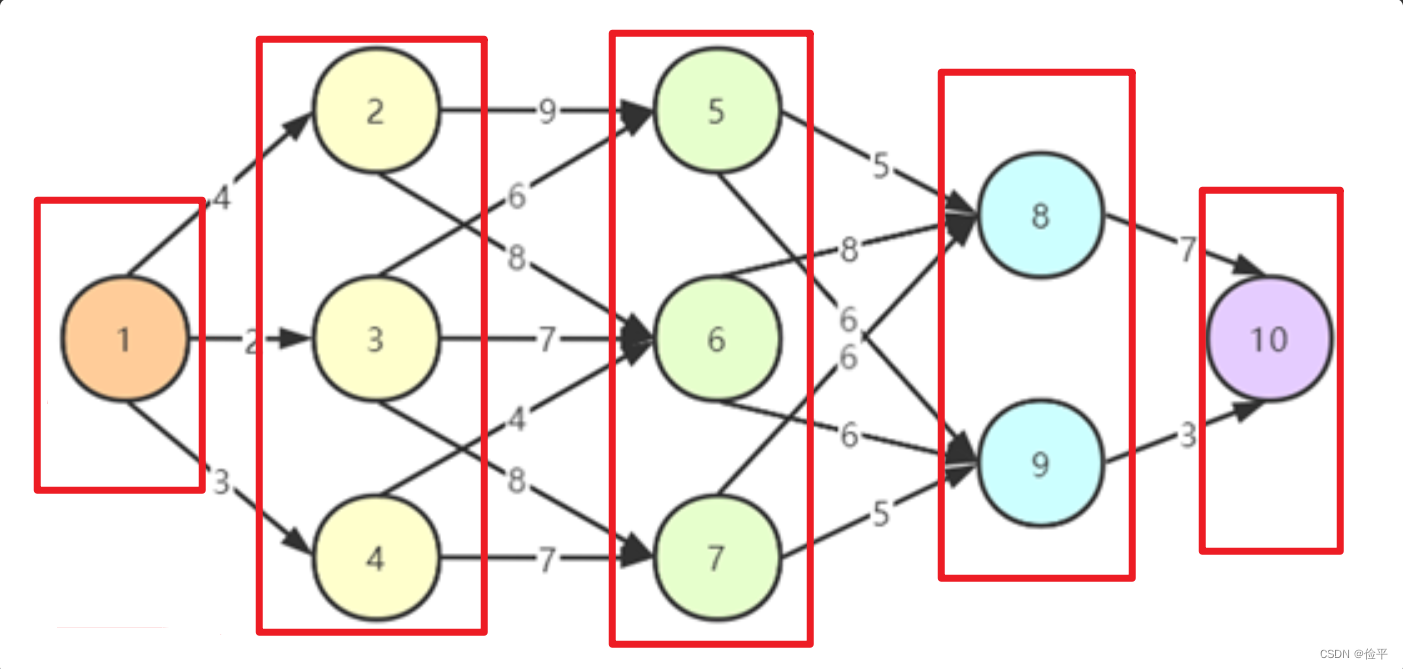
应用：

多段图的最短路径问题：

​ 首先它是个最短路径问题，其次其中的多段的意思，是将图在先不考虑边的情况下，将顶点们分成几个部分。请添加图片描述

如上图所示将图分为了五个部分，也就是分成了5段，分成多个段的目的其实与动态规划解决问题的特性——多阶段是契合的。

核心思想：

我们可以把情况从特殊推广到一般情况，设 Cuv 为多段图有向边 <u,v> 的权值，源点 s 到终点 v 的最短路径长为 d(s,v)，终点为 t，则可以得到该问题的状态转移方程为：

img

详细解读：

以上为理论解释，但是不够直观，接下来我用通俗易懂的方式解释一下：

先解释几个定义，以便我们叙述

d(1,6):从0到6的最短路径，换个角度看我们可以叫他：非直接路径

c(1,2):从1到2的路径，例如c(2,5)=9，同上我们可以叫他：直接路径

先说一个结论：直接路径是确定的，非直接路径是需要求最小值的。

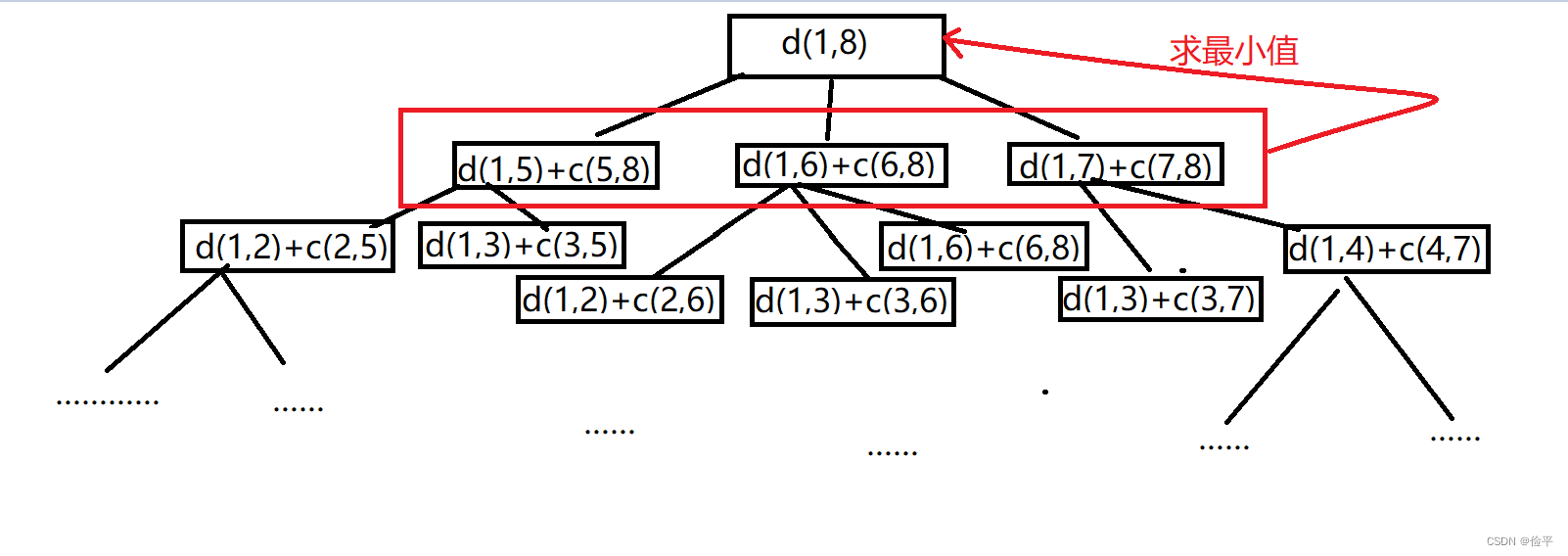
我们用图中一个应用来解释，比如说我们现在要从1走到8，求最短路径d(1,8)，那么应该怎么求呢？首先要考虑的一个问题是既然我们要走到8，那哪些点可以直接到8呢？站在8的位置一看，哦！5、6、7这三个点可以到8，因此确定的是c(5,8)=5、c(6,8)=8、c(7,8)=6，此时从1走到8有三种情况

  • 1——5——8
  • 1——6——8
  • 1——7——8

因此只要我们知道d(1,5)、d(1,6)、d(1,7)便可以用**d(1,5)+c(5,8)**求出1——5——8，剩下两个以此类推，那么接下来的问题就是求d(1,5)了，这显然这跟我们正在求的d(1,8)本质是一样的。那接下来就是分别站在5,6,7的位置重复这一流程。

最后在分别求出d(1,5)+c(5,8)以及其他两个之后，比较三者取最值即可。

可以画一个树来表示整个过程:

img

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<iostream>
#include<algorithm>
#include<stdio.h>
#define Max 0xffff
using namespace std;
//动态规划求最短路径
void dp_path(int c[][100], int *cost, int *path) {
    int m, n;
    cout << "输入顶点个数和边个数" << endl;
    cin >> n >> m;
    //初始化代价矩阵
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            c[i][j] = Max;
    //输入代价矩阵
    int u, v, s;
    for (int i = 0; i < m; i++) {
        cin >> u >> v >> s;
        //cout<<u<<v<<s<<endl;
        c[u][v] = s;
    }
    for(int i=0;i<n;i++)
        cost[i]=Max;
    path[0] = -1;
    cost[0] = 0;
    for (int j = 1; j < n; j++) {
        for (int i = j-1; i >=0; i--) {
            if (cost[j] > cost[i] + c[i][j]) {
                path[j] = i;
                cost[j] = cost[i] + c[i][j];
            }
        }
    }
    cout<<cost[n-1]<<endl;
    int i=path[n-1];
    cout<<path[n-1]<<endl;
    while(path[i]>=0){
        cout<<path[i]<<endl;
        i=path[i];
    }
}
int main()
{
    int c[100][100], cost[100], path[100];
    dp_path(c, cost, path);
    getchar();
    return 0;
}

总结：

此算法的时间复杂度主要由两部分组成：第一部分是依次计算从源点到各个顶点的最短路径长度，由两层嵌套的循环组成，外层循环执行 n-1 次，内层循环对所有入边进行计算，并且在所有循环中，每条入边只计算一次。若假定图的边数为 m，则时间性能是 O(m)。第二部分是输出最短路径经过的顶点，设多段图划分为 k 段，其时间性能是 O(k)。综上所述，**时间复杂度为 O(m+k)**。

许多导航和地图软件，只需要输入起始点和目的点，系统便会给出到达目的地的最短路线，这是多段图最短路径问题的典型应用。

01背包问题：
最长公共子序列问题：

​ 公共就是你有我也有，子序列就是字符串中不一定连续但先后顺序一致的n个字符， 例如字符串abcbca，aca、abba就属于它的子序列；（这里要区别一下子串， 子串：指的是字符串中连续的n个字符 ，例如字符串qwerabc中，qwe、rab、wera都属于它的子串）那么连起来就是：你我都有的最长的不一定连续但先后顺序一致字符串。

例如： 序列1,3,5,4,2,6,8,7和序列1,4,8,6,7,5，它们的最长公共子序列有1,4,8,7和1,4,6,7 ， 其长度是4， 并且通过这个应用我们可以发现，最长公共子序列不一定唯一。

核心思想：

首先我们想解决这个问题，下意识想到的就是无脑遍历啦，但是遍历的时间复杂度太高了，所以不推荐，采用动态规划做有几个点比较重要，那就是动态规划函数的理解

详细解读：

请添加图片描述

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include<iostream>
#include<vector>
#include<algorithm>
#include<string>
using namespace std;
int table[100][100] = { 0 };
int judge[100][100] = { 0 };
int print_LCS(int judge[][100], string x,int,int);
int main()
{
	string a, b;
	cin >> a >> b;
	int m = a.length();
	int n = b.length();
	for (int i = 1; i <= m; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			if (a[i] == b[j])
			{
				table[i][j] = table[i - 1][j - 1] + 1;
				judge[i][j] = 1;	//最后一个字符相等，则
			}
			else if(table[i - 1][j] >= table[i][j - 1])		//最后一个字符不相等，且上方大于左方
			{
				table[i][j] = table[i - 1][j];
				judge[i][j] = 2;
			}
			else
                //最后一个字符不相等，且上方小于左方
			{
				table[i][j] = table[i][j - 1];
				judge[i][j] = 3;
			}
		}
	}
	cout << table[m][n] << endl;
	print_LCS(judge, a, m, n);
	cout << endl;
	system("pause");
}
int print_LCS(int judge[][100],string a,int x,int y)//x,y,分别为两段长度
{
	if (x == 0 || y == 0)
	{
		return 0;
	}
	if (judge[x][y] == 1)
	{
		print_LCS(judge, a, x-1, y-1);
		cout << a[x-1];
	}
	if (judge[x][y] == 2)
	{
		print_LCS(judge, a, x - 1, y);
	}
	if (judge[x][y] == 3)
	{
		print_LCS(judge, a, x, y - 1);
	}
}

总结：

此算法时间复杂度为O(n×m)，其中n为第一个字符串的个数，m为第二个字符串的个数。

最长公共子序列是一个十分实用的问题，它可以描述两段文字之间的“相似度”，即它们的雷同程度，从而能够用来辨别抄袭。对一段文字进行修改之后，计算改动前后文字的最长公共子序列，将除此子序列外的部分提取出来，这种方法判断修改的部分，往往十分准确。简而言之，百度知道、百度百科都用得上。如判断S1和S2相似的办法是找出他们的公共子序列S3，S3以相同的顺序在S1和S2中出现，但是不必要连续。S3越长，S1和S3就越相似。

两个字符串A与B，如果他们最后一个字符是相同的，则此时的最长公共子序列是去掉它们相同的那个，用之前的最长公共子序列长度+1则是，此时的最长公共子序列的长度；如果他们最后一个字符不相同，则此时用A去掉最后一个字符和B求最长公共子序列，再用B去掉最后一个字符和A求最长公共子序列，将两个最长公共子序列作比较，哪个长取哪个。

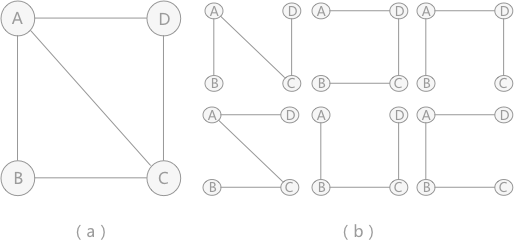
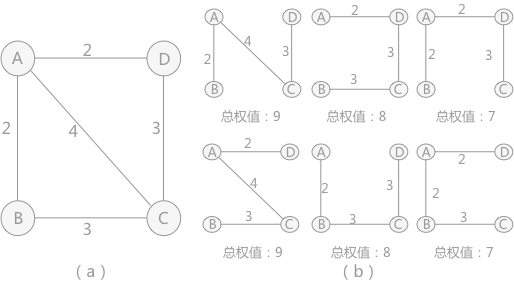
最小生成树问题：

对于含有 n 个顶点的连通图来说可能包含有多种生成树，例如图所示 ：

img

在给定一张无向图，如果在它的子图中，任意两个顶点都是互相连通，并且是一个树结构，那么这棵树叫做生成树。当连接顶点之间的图有权重时，权重之和最小的树结构为最小生成树！

img

在实际中，这种算法的应用非常广泛，比如我们需要在n个城市铺设电缆，则需要n-1条通信线路，那么我们如何铺设可以使得电缆最短呢？最小生成树就是为了解决这个问题而诞生的！

核心思想：

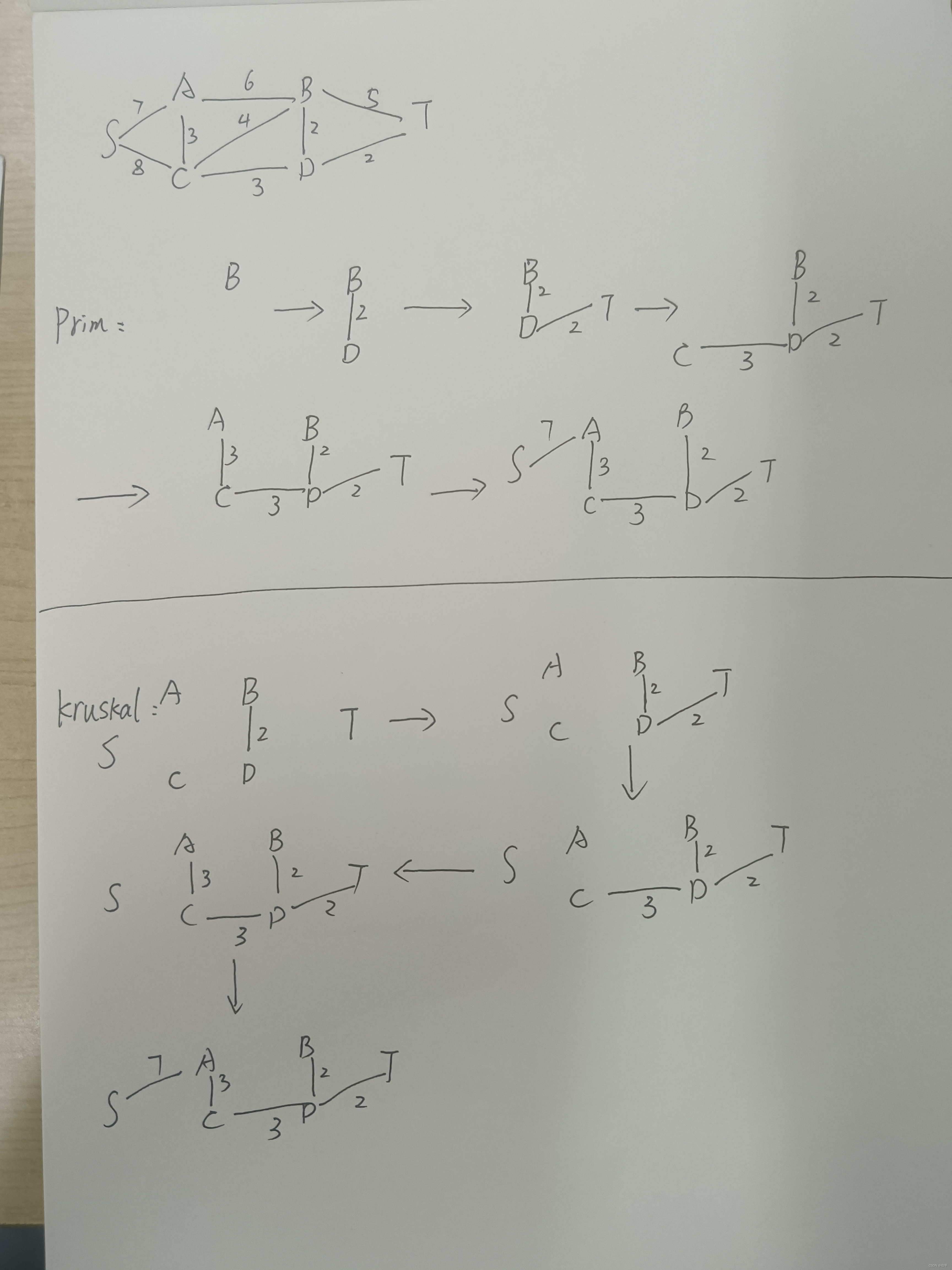
  1. Prim算法（从点出发）

    任选一个顶点，并以此建立生成树的根节点，每一步的贪心选择是把不再生成树中的最近顶点添加到生成树中。

  2. Kruskal算法（从边出发）

    将无向连通图去边，然后在边的权值中选择最小的，然后将这条边的两个顶点相连，再寻找权值最小的，然后将对应顶点相连，直到形成一个生成树（没有闭环）。

详细解读：

请添加图片描述

代码：****

Prim算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include<stdio.h>
#define V 6    // 记录图中顶点的个数
typedef enum { false, true } bool;
//查找权值最小的、尚未被选择的顶点，key 数组记录了各顶点之间的权值数据，visited数组记录着各个顶点是否已经被选择的信息
int min_Key(int key[], bool visited[])
{
    int min = 2147483647, min_index;  //遍历 key 数组使用，min 记录最小的权值，min_index 记录最小权值关联的顶点
    //遍历 key 数组
    for (int v = 0; v < V; v++) {
        //如果当前顶点为被选择，且对应的权值小于 min 值
        if (visited[v] == false && key[v] < min) {
            //更新  min 的值并记录该顶点的位置
            min = key[v];
            min_index = v;
        }
    }
    //返回最小权值的顶点的位置
    return min_index;
}
//输出最小生成树
void print_MST(int parent[], int cost[V][V])
{
    int minCost = 0;
    printf("最小生成树为：\n");
    //遍历 parent 数组
    for (int i = 1; i < V; i++) {
        //parent 数组下标值表示各个顶点，各个下标对应的值为该顶点的父节点
        printf("%d - %d wight:%d\n", parent[i] + 1, i + 1, cost[i][parent[i]]);//由于数组下标从 0 开始，因此输出时各自 +1
        //统计最小生成树的总权值
        minCost += cost[i][parent[i]];
    }
    printf("总权值为：%d", minCost);
}
//根据用户提供了图的信息（存储在 cost 数组中），寻找最小生成树
void find_MST(int cost[V][V])
{    //key 数组用于记录 B 类顶点到 A 类顶点的权值
    //parent 数组用于记录最小生成树中各个顶点父节点的位置，便于最终生成最小生成树
    //visited 数组用于记录各个顶点属于 A 类还是 B 类
    int parent[V], key[V];
    bool visited[V];
    // 初始化 3 个数组
    for (int i = 0; i < V; i++) {
        key[i] = 2147483647;    // 将 key 数组各个位置设置为无限大的数
        visited[i] = false;     // 所有的顶点全部属于 B 类
        parent[i] = -1;         // 所有顶点都没有父节点
    }
    // 选择 key 数组中第一个顶点，开始寻找最小生成树
    key[0] = 0;  // 该顶点对应的权值设为 0
    parent[0] = -1; // 该顶点没有父节点
    // 对于 V 个顶点的图，最需选择 V-1 条路径，即可构成最小生成树
    for (int x = 0; x < V - 1; x++)
    {
        // 从 key 数组中找到权值最小的顶点所在的位置
        int u = min_Key(key, visited);
        // 该顶点划分到 A 类
        visited[u] = true;
        // 由于新顶点加入 A 类，因此需要更新 key 数组中的数据
        for (int v = 0; v < V; v++)
        {
            // 如果类 B 中存在到下标为 u 的顶点的权值比 key 数组中记录的权值还小，表明新顶点的加入，使得类 B 到类 A 顶点的权值有了更好的选择
            if (cost[u][v] != 0 && visited[v] == false && cost[u][v] < key[v])
            {
                // 更新 parent 数组记录的各个顶点父节点的信息
                parent[v] = u;
                // 更新 key 数组
                key[v] = cost[u][v];
            }
        }
    }
    //根据 parent 记录的各个顶点父节点的信息，输出寻找到的最小生成树
    print_MST(parent, cost);
}
// main function
int main()
{
    int p1, p2;
    int wight;
    int cost[V][V] = { 0 };
    printf("输入图（顶点到顶点的路径和权值)：\n");
    while (1) {
        scanf("%d %d", &p1, &p2);
        //如果用户输入 -1 -1，表示输入结束
        if (p1 == -1 && p2 == -1) {
            break;
        }
        scanf("%d", &wight);
        cost[p1 - 1][p2 - 1] = wight;
        cost[p2 - 1][p1 - 1] = wight;
    }
    // 根据用户输入的图的信息，寻找最小生成树
    find_MST(cost);
    return 0;
}

Kruskal算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include <stdio.h>
#include <stdlib.h>
#define N 9   // 图中边的数量
#define P 6   // 图中顶点的数量
//构建表示边的结构体
struct edge {
    //一条边有 2 个顶点
    int initial;
    int end;
    //边的权值
    int weight;
};

//qsort排序函数中使用，使edges结构体中的边按照权值大小升序排序
int cmp(const void* a, const void* b) {
    return  ((struct edge*)a)->weight - ((struct edge*)b)->weight;
}
//克鲁斯卡尔算法寻找最小生成树，edges 存储用户输入的图的各个边，minTree 用于记录组成最小生成树的各个边
void kruskal_MinTree(struct edge edges[], struct edge minTree[]) {
    int i, initial, end, elem, k;
    //每个顶点配置一个标记值
    int assists[P];
    int num = 0;
    //初始状态下，每个顶点的标记都不相同
    for (i = 0; i < P; i++) {
        assists[i] = i;
    }
    //根据权值，对所有边进行升序排序
    qsort(edges, N, sizeof(edges[0]), cmp);
    //遍历所有的边
    for (i = 0; i < N; i++) {
        //找到当前边的两个顶点在 assists 数组中的位置下标
        initial = edges[i].initial - 1;
        end = edges[i].end - 1;
        //如果顶点位置存在且顶点的标记不同，说明不在一个集合中，不会产生回路
        if (assists[initial] != assists[end]) {
            //记录该边，作为最小生成树的组成部分
            minTree[num] = edges[i];
            //计数+1
            num++;
            elem = assists[end];
            //将新加入生成树的顶点标记全部改为一样的
            for (k = 0; k < P; k++) {
                if (assists[k] == elem) {
                    assists[k] = assists[initial];
                }
            }
            //如果选择的边的数量和顶点数相差1，证明最小生成树已经形成，退出循环
            if (num == P - 1) {
                break;
            }
        }
    }
}

void display(struct edge minTree[]) {
    int cost = 0, i;
    printf("最小生成树为:\n");
    for (i = 0; i < P - 1; i++) {
        printf("%d-%d  权值：%d\n", minTree[i].initial, minTree[i].end, minTree[i].weight);
        cost += minTree[i].weight;
    }
    printf("总权值为：%d", cost);
}

int main() {
    int i;
    struct edge edges[N], minTree[P - 1];
    for (i = 0; i < N; i++) {
        scanf("%d %d %d", &edges[i].initial, &edges[i].end, &edges[i].weight);
    }
    kruskal_MinTree(edges, minTree);
    display(minTree);
    return 0;
}

总结：

由于Kruksal算法是对边进行操作，先取出边，然后判断边的两个节点，这样的话，如果一个图结构非常的稠密，那么Kruksal算法就比较慢了，而Prim算法只是对节点进行遍历，并使用set进行标记，因此会相对于Kruksal算法，在稠密图方面好很多，因此Kruksal算法常用于稀疏图，而Prim算法常用于稠密图！

普里姆算法该算法运行的时间复杂度为：O(n^2)，

基于搜索的算法设计技术

回溯法与分支限界法

基本思路：

在这之前我们先看一下解空间树这个概念，因为这两种算法都用到了解空间树

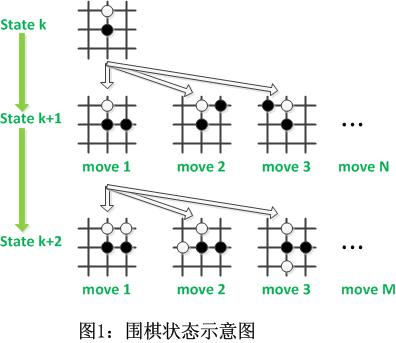
一般来说，当一个问题有多种解，我们表示多种解的时，便可以用到解空间树，说彻底一点其实就是这个问题的解有哪几种情况。

v2-9ff7e1d3a9f80e1309d07aa08fc3d9b9_b

例如上图中，黑白双方各下一子之后，该黑方走棋，此时便有三种情况，move1，move2，move3,，而之后又该白方走棋，白方又有若干种情况，这便构成了下棋这个问题的解空间树。

回溯法：

​ 把问题的解用解空间树的结构表示，然后使用深度优先搜索策略进行遍历，遍历的过程 ：首先从根节点出发搜索解空间树，当算法搜索至解空间树的某一节点时，先利用约束条件判断该节点是否可行（即能得到问题的解）。如果不可行，则对该节点的子树进行剪枝（ 为了避免无效的搜索 ），然后逐层向其祖先节点回溯；否则，进入该子树，继续按深度优先策略搜索。

分支限界法：

​ 把问题的解用解空间树的结构表示， 按广度优先搜索策略搜索问题的解空间树，在搜索过程中，对待处理的节点根据限界函数估算目标函数的可能取值，从中选取使目标函数取得极值（极大或极小）的结点优先进行广度优先搜索，从而不断调整搜索方向（跳跃式），尽快找到问题的解。分支限界法适合求解最优化问题。

​ 用分支限界法解决问题，我们一般有五个步骤：

  1. 确定限界函数
  2. 确定上下界
  3. 利用广度优先扩展结点（把一个结点的所有子结点扩展完）
  4. 根据限界函数评估每一个结点
  5. 结点评估值属于上下界，则加入PT表，不属于则剪枝
  6. 根据所求问题，比较这一层PT表中的结点哪个最大，或者哪个最小来选择结点进行扩展，为什么是这一层呢？因为使用的是广度优先搜索策略

同与异：

同：

  1. 都是基于搜索的算法
  2. 都需要在解空间树中进行搜索
  3. 在搜索的过程中都
  4. 需要进行剪枝

异：

  • 回溯法用深度优先算法（DFS），分支限界法用广度优先算法（BFS）。
  • 回溯法的整个搜索过程是机械的进行，而分支限界法对节点的处理是跳跃式的，因此需要维护一个待处理结点表PT，而PT表的逻辑结构可以用堆或优先队列的形式存储。

适用范围：

回溯法：找到一组可行解，适用于求解组合数较大的问题

分支限界法：找到一组最优解，适合解决最优化问题。

应用：

回溯法和分支限界法实际上都属于蛮力穷举法，在最坏情况下，时间复杂度肯定为指数阶，但是因为其剪枝的特性，只要设计好了约束条件和限界函数，便可以得到不错的时间性能。

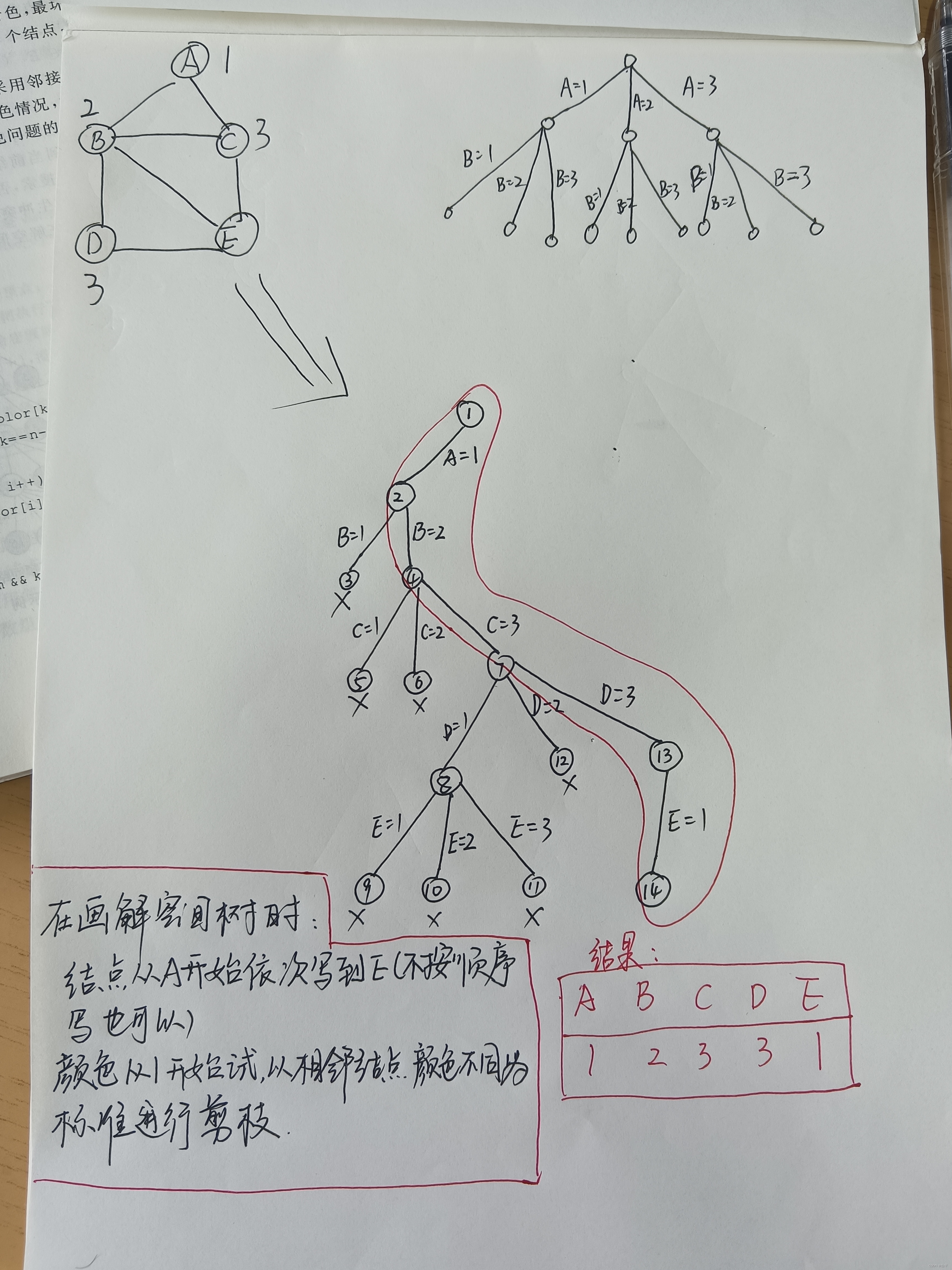
图着色问题：

顾名思义对图中的顶点进行着色的问题，有两个条件，一：图是无向连通图，二：着色时使任意两个相邻顶点着色不同，最后求顶点的涂色情况。

核心思想

在包含问题的所有解的解空间树中，按照深度优先搜索的策略，从根结点出发深度探索解空间树。当探索到某一结点时，要先判断该结点是否包含问题的解，如果包含，就从该结点出发继续探索下去，如果该结点不包含问题的解，则逐层向其祖先结点回溯。（其实回溯法就是对隐式图的深度优先搜索算法）。若用回溯法求问题的所有解时，要回溯到根，且根结点的所有可行的子树都要已被搜索遍才结束。而若使用回溯法求任一个解时，只要搜索到问题的一个解就可以结束。

详细解读

请添加图片描述

1、2、3代表颜色，A\B\C\D\E代表无向连通图中的顶点，1~14代表树中结点的编号。

画出解空间树的过程，或者说解空间树表示的意义就是：在模拟我们对顶点着色的过程，着色必定要一个一个尝试，符合条件保留，不符合剪枝，如果所有颜色都尝试过之后，依旧不符合条件，则回溯到当前结点的父节点处，再进行尝试。

总结

用m种颜色为一个具有n个顶点的无向图着色，共有m^n种可能的着色组合，因此最坏情况下的时间复杂度为O(m^n).

哈密顿回路问题

核心思想

详细解读

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
int arc[10][10];

void Hamiton(int x[], int n) {
	int i, k;
	int visited[10];		//假设图中最多有10个顶点
	for (i = 0; i < n; i++) {
		x[i] = 0;			//初始化回路的顶点数组和标志数组
		visited[i] = 0;
	}
	x[0] = 0;		//从顶点0出发
	visited[0] = 1;
	k = 1;

	while (k >= 1) {
		x[k] = x[k] + 1;	//搜索下一个顶点
		while (x[k] < n) {
			if (visited[x[k]] == 0 && arc[x[k - 1]][x[k]] == 1) {
				break;
			}
			else {
				x[k] = x[k] + 1;
			}
		}

		if (x[k] < n && k == n - 1 && arc[x[k]][0] == 1) {
			for (k = 0; k < n; k++) {
				cout << x[k] + 1 << " ";		//输出顶点的编号，从1开始
			}
			return;
		}
		if (x[k] < n && k < n - 1) {
			visited[x[k]] = 1;
			k = k + 1;
		}
		else {							//回溯
			visited[x[k]] = 0;
			x[k] = 0;
			k = k - 1;
		}
	}
}

总结

TSP问题：

TSP，即旅行商问题，又称TSP问题（Traveling Salesman Problem）， 假设有一个旅行商人要拜访N个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。TSP问题是一个NPC问题。

img

核心思想

在这里插入图片描述

很明显，这表达太抽象了！

img

详细解读：

可以看看这个视频吧，说的比较清楚，可能有点啰嗦了。。

TSP问题——分支限界法

完整流程就是，

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302

import java.util.*;

class Node implements Comparable{
    int[] visp;//标记哪些点走了
    int st;//起点
    int ed;//终点
    int k;//走过的点数
    int sumv;//经过路径的距离
    int lb;//目标函数的值
    Map<Integer,Integer> map_edge=new HashMap<>();//记录已经加入的边

    @Override
    public int compareTo(Object o){
        Node node=(Node) o;
        if(node.lb<this.lb)
            return 1;
        else if(node.lb>this.lb)
            return -1;
        return 0;
    }
}
public class BBTSP {
    private int[][] mp;
    int n;
    int up=16;//路径总和上界,第一次为无穷大，后面取每个可行分支的最小值
    int low;//路径和最小值
    private List<Point> points;
    private PriorityQueue<Node> q=new PriorityQueue<>();
    private PriorityQueue<Node> q_last=new PriorityQueue<>();//记录每条路径的最后一个节点，以及对应的路径值

    public BBTSP(int[][] mp,List<Point> points){
        this.mp=mp;
        points=this.points;
        n=points.size();
        sum_origin=points.get(0).getStock();
    }

    public BBTSP(int[][] mp){
       this.mp=mp;
        n=5;
    }

    void get_low()
    {
        low=0;
        for(int i=0; i<n; i++)
        {
        /*通过排序求两个最小值*/
            //double min1=Double.MAX_VALUE,min2=Double.MAX_VALUE;
            double[] tmpA=new double[n];
            for(int j=0; j<n; j++)
            {
                //if(i==j) continue;
                tmpA[j]=mp[i][j];
            }
           Arrays.sort(tmpA);//对临时的数组进行排序
            low+=tmpA[1]+tmpA[2];

        }
        low=low%2==0?low/2:(low/2+1);
    }

    public int get_lb(Node p){
        int ret=p.sumv*2;//路径上的点的距离
        double min1=Double.MAX_VALUE,min2=Double.MAX_VALUE;//起点和终点连出来的边
       /* System.out.println("边：");
        for(Map.Entry<Integer,Integer> entry: p.map_edge.entrySet())
            System.out.println("start="+entry.getKey()+",end="+entry.getValue());*/
        Map<Integer,Integer> map=p.map_edge;

        for(int i=0; i<n; i++) {
           // System.out.println("++++++++++++i="+i+"+++++++++++++++++++");
            boolean flag1 = false;//该点为出点
            boolean flag2 = false;//该点为入点

            int end = -1;
            int start = -1;

            if (map.containsKey(i)) {
                flag1 = true;
                end = map.get(i);
            }
            if (map.containsValue(i)) {
                flag2 = true;
                for(Map.Entry<Integer,Integer> entry:map.entrySet())
                    if(entry.getValue()==i) start=entry.getKey();
            }
            if (flag1 && flag2) continue;

            List<Integer> array=new ArrayList<>();
            if (!flag1&&flag2) {//该点只有入点，没有出点
                for (int j = 0; j < n; j++) {
                    if (i == j || j == start) continue;
                    array.add(mp[i][j]);
                    //System.out.println("flag1       map["+i+"]"+"["+j+"]="+mp[i][j]);
                }
                Collections.sort(array);

                ret += array.get(0);
               // System.out.println("array.get(0)="+array.get(0)+",ret="+ret);
            }

            if (!flag2&&flag1) {
                array=new ArrayList<>();
                for (int j = 0; j < n; j++) {
                    if (i == j || j == end) continue;
                    array.add(mp[j][i]);
                    //System.out.println("flag2       map["+j+"]"+"["+i+"]="+mp[j][i]);
                }
                Collections.sort(array);
                ret += array.get(0);
                //System.out.println("array.get(0)="+array.get(0)+",ret="+ret);
            }

            if(!flag1&&!flag2){
                array=new ArrayList<>();
                for (int j = 0; j < n; j++) {
                    if (i == j) continue;
                    array.add(mp[i][j]);
                }
                Collections.sort(array);
                ret += array.get(0)+array.get(1);
               // System.out.println("array.get(0)="+array.get(0)+"array.get(1)="+array.get(1)+",ret="+ret);
            }


        }
        System.out.println("2.ret="+ret);
        return ret%2==0?(ret/2):(ret/2+1);
    }

    public Node solve(){
        get_low();
        System.out.println("low="+low);
        /*设置初始点,默认从1开始 */
        Node star=new Node();
        star.st=0;
        star.ed=0;
        star.k=1;
        star.visp=new int[n];
        for(int i=0; i<n; i++) star.visp[i]=0;
        star.visp[0]=1;
        star.sumv=0;
        star.lb=low;
        System.out.println("n="+n);
        /*ret为问题的解*/
        double ret=Double.MAX_VALUE;

        q.add(star);
        while(!q.isEmpty())
        {
            Node tmp=q.peek();

            if(!q_last.isEmpty()){
                Node last=q_last.peek();
                if(last.lb<=tmp.lb) return last;
            }
            System.out.println("输出队列里面的数据");
            Iterator<Node> it=q.iterator();
            while (it.hasNext()){
                Node no=it.next();
                System.out.println("node.st="+no.st+";node.ed="+no.ed+";node.sumv="+no.sumv);
            }
            System.out.println("--------------------------------------------------------");
            System.out.println("tmp.st="+tmp.st+";tmp.ed="+tmp.ed+";tmp.sumv="+tmp.sumv);
            Map<Integer,Integer> tmp_map=tmp.map_edge;
            q.poll();
            if(tmp.k==n-1)
            {
                System.out.println("最后一个点");
            /*找最后一个没有走的点*/
                int p=0;
                for(int i=0; i<n; i++)
                {
                    if(tmp.visp[i]==0)
                    {
                        p=i;
                        break;
                    }
                }

                Node next=new Node();
                next.visp=new int[n];
                next.st=tmp.ed;
                next.ed=p;
                int ans=tmp.sumv+mp[p][0]+mp[tmp.ed][p];//最终的最短路径
                next.sumv=ans;
                next.k=tmp.k+1;
                next.map_edge.putAll(tmp.map_edge);
                next.map_edge.put(next.st,next.ed);
                next.map_edge.put(next.ed,0);
                next.lb=ans;
                System.out.println("next.i="+p+";next.lib="+next.lb+";next.st="+next.st+";next.ed="+next.ed+";next.sumv="+next.sumv);
                Node judge = q.peek();
                /*如果当前的路径和比所有的目标函数值都小则跳出*/
                if(ans <= judge.lb||judge==null)
                {
                    //ret=Math.min(ans,ret);
                   // ret_map.put(ans,next);
                    return next;
                   // break;
                }
               /*否则继续求其他可能的路径和，并更新上界*/
                else
                {
                    up = Math.min(up,ans);
                    q_last.add(next);
                   // ret=Math.min(ret,ans);
                    continue;
                }
            }
        /*当前点可以向下扩展的点入优先级队列*/

            for(int i=0; i<n; i++)
            {
                if(tmp.visp[i]==0)
                {
                    Node next=new Node();
                    next.visp=new int[n];
                    next.st=tmp.ed;

                /*更新路径和*/
                    //System.out.println("tmp.sumv="+tmp.sumv);
                    next.sumv=tmp.sumv+mp[tmp.ed][i];

                /*更新最后一个点*/
                    next.ed=i;

                /*更新顶点数*/
                    next.k=tmp.k+1;

                /*更新经过的顶点*/
                    for(int j=0; j<n; j++) next.visp[j]=tmp.visp[j];
                    next.visp[i]=1;

                /*求目标函数*/
                    Map<Integer,Integer> next_map=new HashMap<>();
                    next_map.putAll(tmp_map);
                    next_map.put(next.st,next.ed);
                    next.map_edge=next_map;

                    next.lb=get_lb(next);
                    System.out.println("sumv="+next.sumv);
                    System.out.println("next.i="+i+";next.lib="+next.lb+";next.st="+next.st+";next.ed="+next.ed+";next.sumv="+next.sumv);

                /*如果大于上界就不加入队列*/

                    if(next.lb>up){
                        next_map.remove(next.st);
                        continue;
                    }
                    q.add(next);
                }
            }
        }
       // return ret;
        return null;
    }

    public static void main(String[] args){
        int[][] d={
                {0,3,1,5,8},
                {3,0,6,7,9},
                {1,6,0,4,2},
                {5,7,4,0,3},
                {8,9,2,3,0}
        };
        BBTSP b=new BBTSP(d);
        Node node=b.solve();
        System.out.println();
        System.out.println("+++++++++++++++++++++++++输出结果：++++++++++++++++++++++++");
        System.out.println("最后遍历的点的信息：");
        System.out.println("node.lib="+node.lb+";node.st="+node.st+";node.ed="+node.ed+";node.sumv="+node.sumv);
        System.out.println("最短路径为："+node.lb);
        System.out.println("构成的边为：");
        for(Map.Entry<Integer,Integer> entry: node.map_edge.entrySet()){
            System.out.println(entry.getKey()+"  ->  "+entry.getValue());
        }
      /*  Node n1=new Node();
        n1.lb=9;
        Node n2=new Node();
        n2.lb=19;
        Node n3=new Node();
        n3.lb=11;
        Node n4=new Node();
        n4.lb=5;
        Node n5=new Node();
        n5.lb=2;
         PriorityQueue<Node> q1=new PriorityQueue<>();
        q1.add(n1);
        q1.add(n2);
        q1.add(n3);
        q1.add(n4);
        q1.add(n5);
        while(!q1.isEmpty()){
            Node nn=q1.poll();
            System.out.println(nn.lb);
        }*/
    }
}

01背包问题
有一个容量为`W`的背包，还有`n`个物体。现在忽略物体实际几何形状，我们认为只要背包的剩余容量大于等于物体体积，那就可以装进背包里。每个物体都有两个属性，即体积`w`和价值`v`。 问：如何向背包装物体才能使背包中物体的总价值最大？

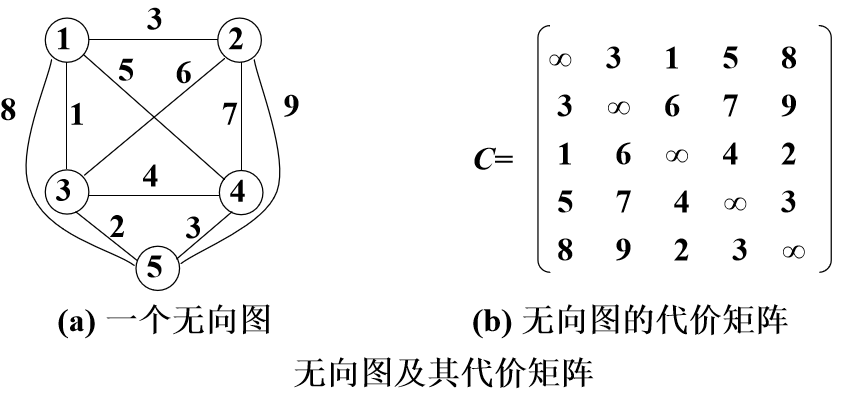
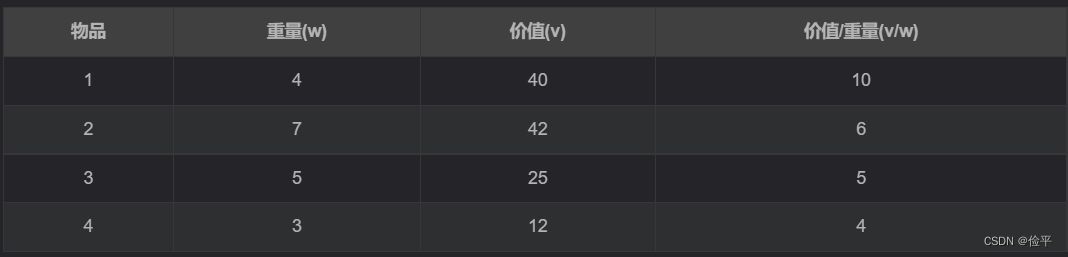
背包容量W=10；物品个数n=4

img

核心思想

一般情况下，假设当前已经对前i个物品进行了某种特定的选择，且背包中已装入物品的重量时w，获得的价值是v，计算该节点的目标函数上界的一个简单方法是，将背包中剩余容量全被装入第i+1个物品，并可以将背包装满，于是得到了限界函数：

在这里插入图片描述

W为背包的容量，物品i的重量时wi，其价值为vi

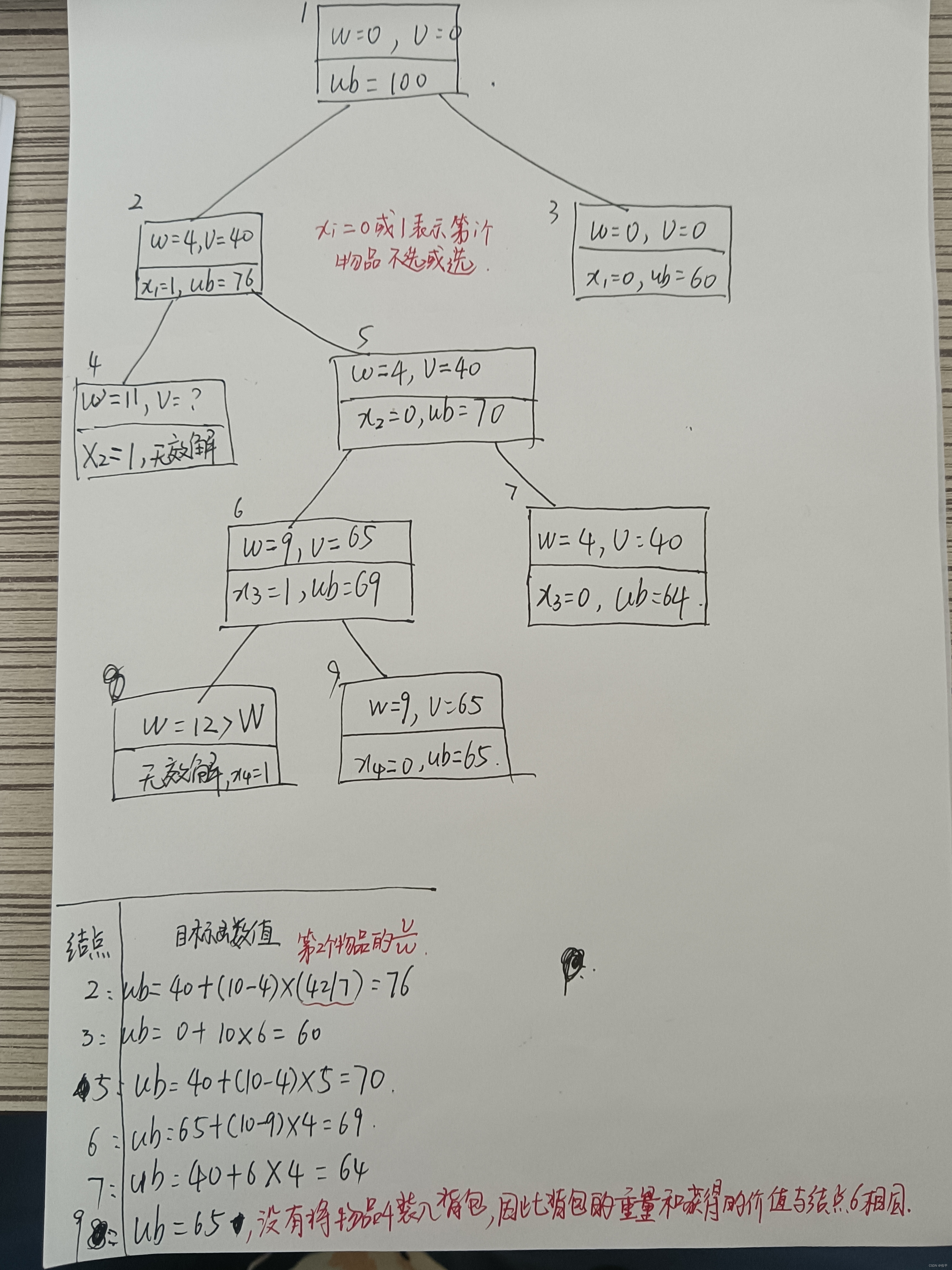
详细解读

img

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <queue>
using namespace std;
const int N = 10;
bool bestx[N];
//定义结点。每个节点来记录当前的解。
struct Node
{
    int cp, rp; //cp背包的物品总价值，rp剩余物品的总价值
    int rw; //剩余容量
    int id; //物品号
    bool x[N];//解向量
    Node() {}
    Node(int _cp, int _rp, int _rw, int _id){
        cp = _cp;
        rp = _rp;
        rw = _rw;
        id = _id;
        memset(x, 0, sizeof(x));//解向量初始化为0
    }
};
struct Goods
{
    int value;
    int weight;
} goods[N];
 
int bestp,W,n,sumw,sumv;
/*
  bestp 用来记录最优解。
  W为购物车最大容量。
  n为物品的个数。
  sumw 为所有物品的总重量。
  sumv 为所有物品的总价值。
*/
//bfs 来进行子集树的搜索。
int bfs()
{
    int t,tcp,trp,trw;
    queue<Node> q; //创建一个普通队列(先进先出)
    q.push(Node(0, sumv, W, 1)); //压入一个初始结点
    while(!q.empty()) //如果队列不空
    {
        Node livenode, lchild, rchild;//定义三个结点型变量
        livenode=q.front();//取出队头元素作为当前扩展结点livenode
        q.pop(); //队头元素出队
        //cp+rp>bestp当前装入的价值+剩余物品价值小于当前最优值时，不再扩展。
        cout<<"当前结点的id值:"<<livenode.id<<"当前结点的cp值:"<<livenode.cp<<endl;
        cout<<"当前结点的解向量:";
        for(int i=1; i<=n; i++)
        {
            cout<<livenode.x[i];
        }
        cout<<endl;
        t=livenode.id;//当前处理的物品序号
        // 搜到最后一个物品的时候不需要往下搜索。
        // 如果当前的购物车没有剩余容量(已经装满)了，不再扩展。
        if(t>n||livenode.rw==0)
        {
            if(livenode.cp>=bestp)//更新最优解和最优值
            {
              for(int i=1; i<=n; i++)
              {
                bestx[i]=livenode.x[i];
              }
              bestp=livenode.cp;
            }
            continue;
        }
        if(livenode.cp+livenode.rp<bestp)//判断当前结点是否满足限界条件，如果不满足不再扩展
          continue;
        //扩展左孩子
        tcp=livenode.cp; //当前购物车中的价值
        trp=livenode.rp-goods[t].value; //不管当前物品装入与否，剩余价值都会减少。
        trw=livenode.rw; //购物车剩余容量
        if(trw>=goods[t].weight) //满足约束条件，可以放入购物车
        {
            lchild.rw=trw-goods[t].weight;
            lchild.cp=tcp+goods[t].value;
            lchild=Node(lchild.cp,trp,lchild.rw,t+1);//传递参数
            for(int i=1;i<t;i++)
            {
              lchild.x[i]=livenode.x[i];//复制以前的解向量
            }
            lchild.x[t]=true;
            if(lchild.cp>bestp)//比最优值大才更新
               bestp=lchild.cp;
            q.push(lchild);//左孩子入队
        }
        //扩展右孩子
        if(tcp+trp>=bestp)//满足限界条件，不放入购物车
        {
            rchild=Node(tcp,trp,trw,t+1);//传递参数
            for(int i=1;i<t;i++)
            {
              rchild.x[i]=livenode.x[i];//复制以前的解向量
            }
            rchild.x[t]=false;
            q.push(rchild);//右孩子入队
        }
    }
    return bestp;//返回最优值。
}
 
int main()
{
    //输入物品的个数和背包的容量
    cout << "请输入物品的个数 n:";
    cin >> n;
    cout << "请输入购物车的容量W:";
    cin >> W;
    cout << "请依次输入每个物品的重量w和价值v,用空格分开:";
    bestp=0; //bestv 用来记录最优解
    sumw=0; //sumw为所有物品的总重量。
    sumv=0;   //sum 为所有物品的总价值
    for(int i=1; i<=n; i++)
    {
        cin >> goods[i].weight >> goods[i].value;//输入第 i 件物品的体积和价值。
        sumw+= goods[i].weight;
        sumv+= goods[i].value;
    }
    if(sumw<=W)
    {
        bestp=sumv;
        cout<<"放入购物车的物品最大价值为: "<<bestp<<endl;
        cout<<"所有的物品均放入购物车。";
        return 0;
    }
    bfs();
    cout<<"放入购物车的物品最大价值为: "<<bestp<<endl;
    cout<<"放入购物车的物品序号为: ";
    // 输出最优解
    for(int i=1; i<=n; i++)
    {
        if(bestx[i])
           cout<<i<<"  ";
    }
    return 0;
}

计算的限制

问题的复杂性

Turing论题：一个问题是可计算的当且仅当它在图灵机上经过有限步骤后得到正确的结果。

停机问题是典型的不可计算问题。

易解问题：将可以在多项式时间（多项式时间复杂度）内求解的问题看做是易解问题，例如：排序问题、串匹配问题。

难解问题：将需要指数时间求解的问题看做是难解问题。例如：汉诺塔问题、TSP问题。

确定性算法：如果该算法在整个执行过程中，每一步只有一个确定的选择，并且对于同一输入实例运行算法，所得的结果严格一致，则称其为确定性算法。

P类问题：其中的P的英文全程是：polynomial，其含义是“多项式”，如果对于某个判断行问题，存在一个正整数k，对于输入规模为n的实例，能够以O（n^k）的时间运行一个确定性算法，得到yes或者no的答案，则称这个问题为P类问题。

常见的基本的NP完全问题：图着色问题、哈密顿回路问题和TSP问题。

问：解决NP完全问题用什么技术？

答：用近似算法和概率算法。

近似算法

基本思路：用近似最优解代替最优解，以换取算法设计上的简化和时间复杂度的降低。换言之，近似算法找到的可能不是一个最优解，但它总会待为求问题提供一个解，为了具有实用性，近似算法必须给出能够给出算法所产生的解与最优解之间的差别。

适用范围：求解NP难问题。

概率算法

基本思路：

允许算法在执行过程中随机选择下一步该怎么走，同时允许结果以较小的概率出现错误，并以此为代价，获得算法运行时间的大幅度减少。

蒙特卡罗型概率算法

蒙特罗卡型概率算法用于求解问题的准确解。

设p是一个实数，且1<1/2<p<1。如果一个蒙特卡罗型概率算法对于问题的任一输入实例得到正确解的概率不小于p，则称该蒙特卡罗型概率算法是p正确的。

拉斯维加斯型概率算法

设p(x)是对输入实例x调用拉斯维加斯型概率算法获得问题的一个解的概率，则一个正确的拉斯维加斯型概率算法应该对于所有的输入实例x均有p(x)>0.

参考地址：

归并排序

快速排序

快速排序

二叉树搜索树

堆排序

二叉查找树

动态规划和贪心算法的异同

多段图的最短路径问题

阿里大佬讲算法

最小生成树

图